As one angle is 90, so this triangle is always a right triangle As explained above that it is a special triangle so it has special values of lengths and angles The basic triangle sides ratio is The side opposite the 30° angle x The side opposite30 60 90 triangle rules and properties The most important rule to remember is that this special right triangle has one right angle and its sides are in an easytoremember consistent relationship with one another the ratio is a a√3 2aTo learn more about Triangles enrol in our full course now https//bitly/Triangles_DMIn this video, we will learn 000 triangle017 proof of 306
1
Right triangle formulas 30 60 90
Right triangle formulas 30 60 90-• area = 05 *Special right triangles hold many applications in both geometry and trigonometry In this lesson you will learn the general formula for the ratios, and how to find missing sides of any 30 60 90 right triangle




30 60 90 Triangle Calculator Formula Rules
Triangles The triangle is one example of a special right triangle It is right triangle whose angles are 30°, 60° and 90° The lengths of the sides of a triangle are in the ratio of 1√32 The following diagram shows a triangle and the ratio of the sides Scroll down the page for more examples andAnswer (1 of 3) This question definitely needs to be edited first I guess the question is Q What is the formula to find the hypotenuse in a 30 60 90 triangle If the question is as above FORMULA HYPOTENUSE = √{ s² (√3 s)²}, where s is a side length of the right triangle And obviou30° 60° 90° x x√3 2x x²√3/2 x(3√3) 30° 60° 45° 45° 90° x x x√2 x²/2 x(2√2) 45° 45° x 2x x 2x x√5 x² x(3√5) ~265° ~635° x 3x x 3x x√10 3x²/2 x(4√10) ~185° ~715° 3x 4x 5x 3x 4x 5x 6x² 12x ~37° ~53°
How To Work With degree Triangles 30 60 90 Triangle If you've had any experience with geometry, you probably know Learn Details about 30 60 90Related Pages Right Triangle Other Special Right Triangles More Geometry Lessons Recognizing special right triangles in geometry can provide a shortcut when answering some questions A special right triangle is a right triangle whose sides are in a particular ratioYou can also use the Pythagorean theorem formula, but if you can see that it is a special triangle it can save The triangle is a special right triangle, and knowing it can save you a lot of time on standardized tests like the SAT and ACT Because its angles and side ratios are consistent, test makers love to incorporate this triangle into problems, especially on the
A triangle is one of the few special right triangles with angles and side ratios that are consistent and predictable Specifically, every triangle has a 30º angle, a 60º angle, and a 90º angle Since these angles stay the same, the ratio between the length of the sides also remains the same 30 60 90 triangle sides If we know the shorter leg length a, we can find out that b = a√3 c = 2a If the longer leg length b is the one parameter given, then a = b√3/3 c = 2b√3/3 For hypotenuse c known, the legs formulas look as follows a = c/2 b = c√3/2 Or simply type your given values and the 30 60 90 triangle calculator will do the rest! Triangle Practice Name_____ ID 1 Date_____ Period____ ©v j2o0c1x5w UKVuVt_at iSGoMfttwPaHrGex rLpLeCkQ l ^AullN Zr\iSgqhotksV vrOeXsWesrWvKe`d\1Find the missing side lengths Leave your answers as radicals in simplest form 1) 12 m n 30° 2) 72 ba 30° 3) x y 5 60° 4) x 133y 60° 5) 23 u v 60° 6) m n63




30 60 90 Triangle Explanation Examples




30 60 90 Triangle Theorem Ratio Formula Video
Special right triangle a (shorter leg) b (longer leg) c (hypotenuse) Area Perimeter Angle α Angle β;The ratio of the sides follow the triangle ratio 1 2 √3 1 2 3 Short side (opposite the 30 30 degree angle) = x x Hypotenuse (opposite the 90 90 degree angle) = 2x 2 x Long side (opposite the 60 60 degree angle) = x√3 x 3Enter 1 out of 3 to solve for the other 2 missing sides Special right triangle 30 60 90 is one of the most popular right triangles The 30 60 90 right triangle is a special case triangle with angles measuring 30 60 and 90 degrees If you want to read more about that special shape check our calculator dedicated to the 30 60 90 triangle



Special Right Triangle 30 60 45 45 37 53 Elearning
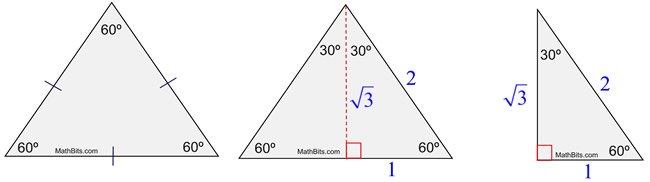



Special Right Triangle 30 60 90 Mathbitsnotebook Geo Ccss Math
Side opposite the 90° angle 2x All degree triangles have sides with the same basic ratio Two of the most common right triangles are and degree triangles If you look at the 30–60–90degree triangle in radians, it translates to the following In any triangle, you see the followingAnswer (1 of 6) Let ABC is a right angled triangle in which hypotenuse AC =6 units ,angle C=30° , angle A=60° and angle B =90° AB/AC=sin30° AB= 6×1/2 = 3 units BC/AC=cos30° BC=6×√3/2=3√3 units or 3×1732 = 5196 units Length of the shortest side (AB) = 3 units Answer Secondmethod The two special right triangles are right triangles with interior angles measuring 30 60 90 and 45 45 90 What is the 45 45 90 triangle rule?



The Easy Guide To The 30 60 90 Triangle




30 60 90 Right Triangle Side Ratios Expii
Special triangles – Formula and examples Special triangles are right triangles that have special proportions for their sides The 30°60°90° triangle has the proportions 1√32 The 45°45°90° triangle has the proportions 11√2 All the lengths of these sides can be easily found if we only know the length of one of the sidesY√3 = Long side (opposite the 60° angle) These three special rules can be considered the triangle theorem and are unique to these special right triangles The hypotenuse (the triangle's longest side) is always twice the length of the short leg The length of the longer leg is the short leg's length times √3In this type of right triangle, the sides corresponding to the angles 30°60°90° follow a ratio of 1√ 3 2 Thus, in this type of triangle, if the length of one side and the side's corresponding angle is known, the length of the other sides can be determined using the above ratio




How To Work With 30 60 90 And 45 45 90 Degree Triangles Dummies




30 60 90 Math Methods Studying Math Physics And Mathematics
The 45 45 90Area of a Triangle The formula to calculate the area of a triangle is = (1/2) × base × height In a rightangled triangle, the height is the perpendicular of the triangle Thus, the formula to calculate the area of a rightangle triangle is = (1/2) × base × perpendicularUse the properties of special right triangles described on this page) Show Answer The 30$$^{\circ}$$ and 60$$^{\circ}$$ angles give this one away x = 6




30 60 90 Special Right Triangle Calculator Inch Calculator




A Quick Guide To The 30 60 90 Degree Triangle Dummies
A triangle is a special right triangle (a right triangle being any triangle that contains a 90 degree angle) that always has degree angles of 30 degrees, 60 degrees, and 90 degrees Because it is a special triangle, it also has side length values which are always in a consistent relationship with one anotherSince this is a right triangle, we know that the sides exist in the proportion 1 √3 3 2 The shortest side, 1, is opposite the 30 degree angle Since side X is opposite the 60 degree angle, we know that it is equal to 1∗ √3 1 ∗ 3, or about 173Special Right Triangles Formulas 30 60 90 and 45 45 90 2 hours ago Mathwarehousecom Visit Site Although all right triangles have special features – trigonometric functions and the Pythagorean theoremThe most frequently studied right triangles, the special right triangles, are the 30, 60, 90 Triangles followed by the 45, 45, 90 triangles See Also Free Catalogs Show more
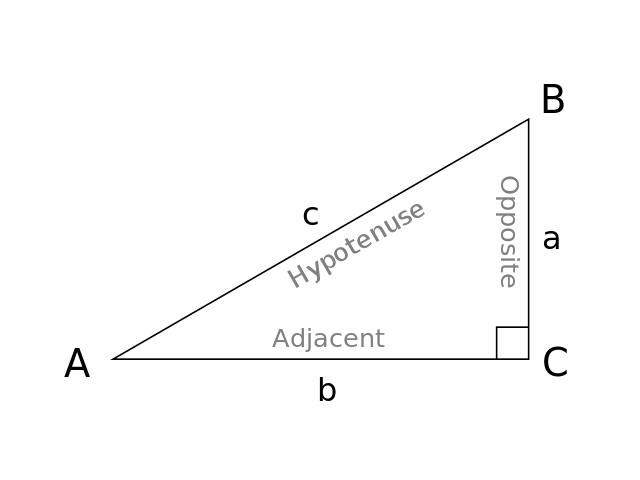



30 60 90 Triangle Formulas Rules And Sides Science Trends
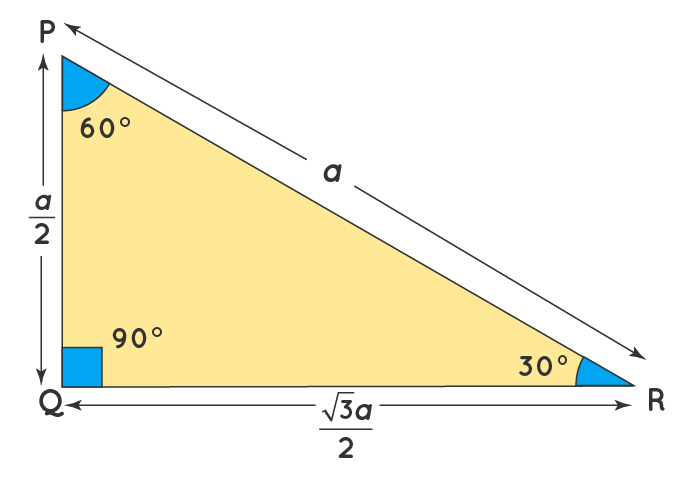



30 60 90 Triangle Definition Theorem Formula Examples
The area of a 30, 60, 90 triangle Hi Willetta The easiest way to calculate the area of a right triangle (a triangle in which one angle is 90 degrees) is to use the formula A = 1/2 b h where b is the base (one of the short sides) and h is the height (the other short side)A 30 60 90 triangle is a special type of right triangle What is special about 30 60 90 triangles is that the sides of the 30 60 90 triangle always have the same ratio Therefore, if we are given one side we are able to easily find the other sides using the ratio of 12square root of threeWatch more videos on http//wwwbrightstormcom/math/geometrySUBSCRIBE FOR All OUR VIDEOS!https//wwwyoutubecom/subscription_center?add_user=brightstorm2VI
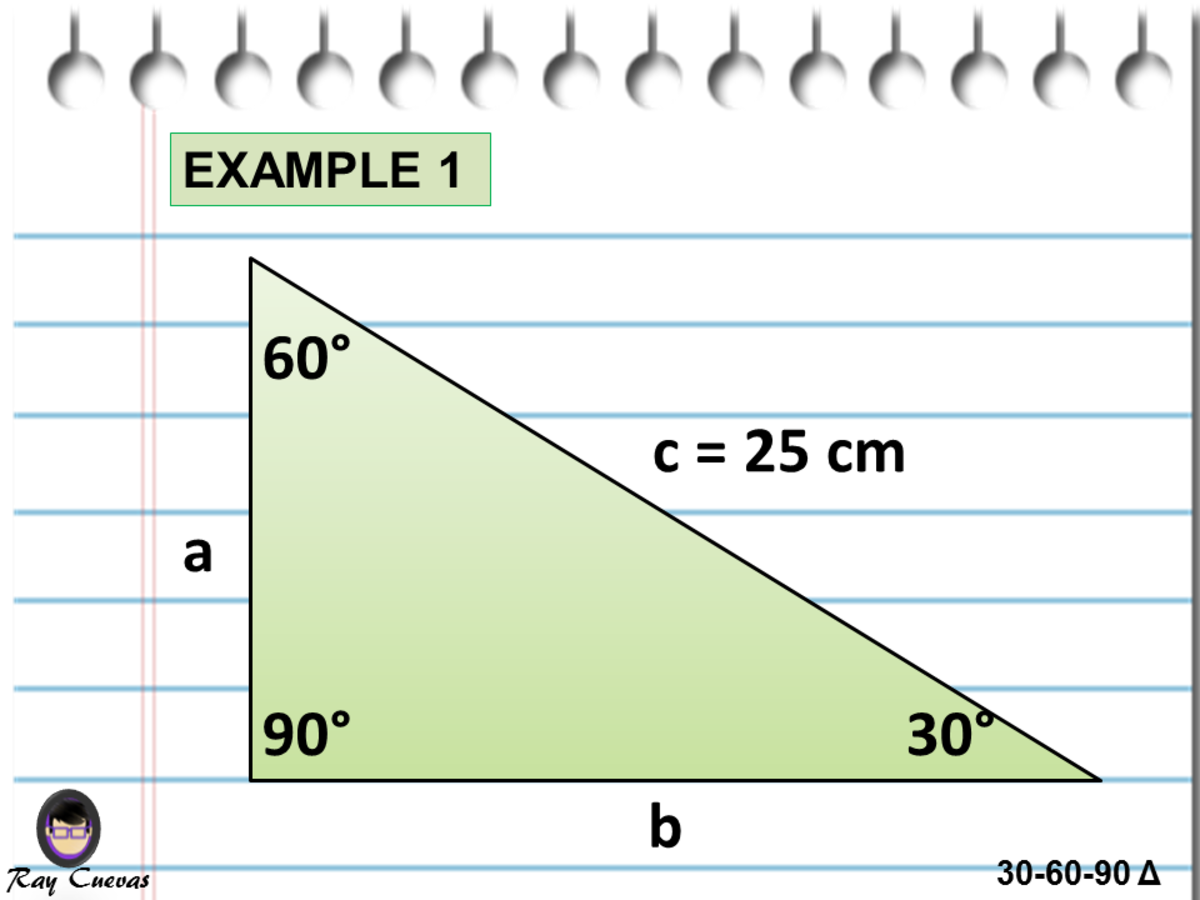



A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation




30 60 90 Triangles Special Right Triangle Trigonometry Youtube
Example We multiply the length of the leg which is 7 inches by √2 to get the length of the hypotenuse $$7\cdot \sqrt{2}\approx 99$$ In a 30°60° right triangle we can find the length of the leg that is opposite the 30° angle by using this formulaA 30̊ 60̊ 90̊ right triangle or rightangled triangle is a triangle with angles 30̊ 60̊ 90̊ Formulas of triangle with angle 30̊ 60̊ 90̊ • perimeter = long side short side hypotenuse; tan (60) = √3/1 = 173 The right triangle is special because it is the only right triangle whose angles are a progression of integer multiples of a single angle If angle A is 30 degrees, the angle B = 2A (60 degrees) and angle C = 3A (90 degrees)




30 60 90 Triangles
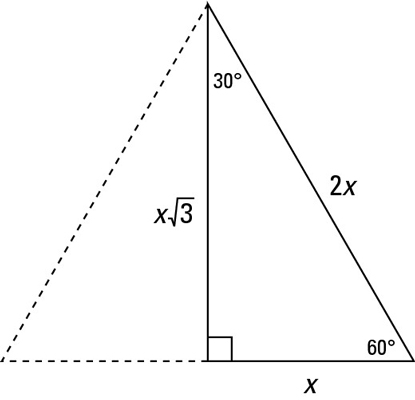



Identifying The 30 60 90 Degree Triangle Dummies
The reason these triangles are considered special is because of the ratios of their sides they are always the same! A triangle is a right triangle with angle measures of 30º, 60º, and 90º (the right angle) Because the angles are always in that ratio,The 30–60–90 Day Plan is a document prepared by a job seeker and presented during an interview It is an outline of what the candidate intends or proposes to achieve in the first 90 days, if hired for the role Beside above, what are the sides of a 30 60 90 Triangle?




30 60 90 Triangle Theorem Ratio Formula Video




30 60 90 Triangle Explanation Examples
THE 30°60°90° TRIANGLE THERE ARE TWO special triangles in trigonometry One is the 30°60°90° triangle The other is the isosceles right triangle They are special because, with simple geometry, we can know the ratios of their sides Theorem In a 30°60°90° triangle the sides are in the ratio 1 2 We will prove that belowA triangle is a right triangle with angle measures of 30º, 60ºA right triangle (literally pronounced "thirty sixty ninety") is a special type of right triangle where the three angles measure 30 degrees, 60 degrees, and 90 degrees The triangle is significant because the sides exist in an easytoremember ratio 1sqrt (3)2 That is to say, the hypotenuse is twice as long as the shorter leg, and




30 60 90 Triangle Theorem Ratio Formula Video
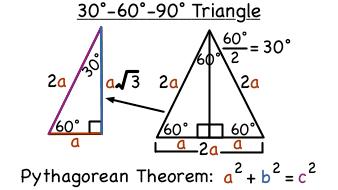



What Is A 30 60 90 Degree Triangle Virtual Nerd
A triangle is a right triangle with angle measures of 30º, 60º, and 90º (the right angle) Because the angles are always in that ratio, the sides are also always in Right triangles are one particular group of triangles and one specific kind of right triangle is a right triangle As the name suggests, the three angles in the triangle are 30, 60If any triangle has its sides in the ratio 1 2 √3, then it is a triangle




30 60 90 Triangle Formulas Rules And Sides Science Trends
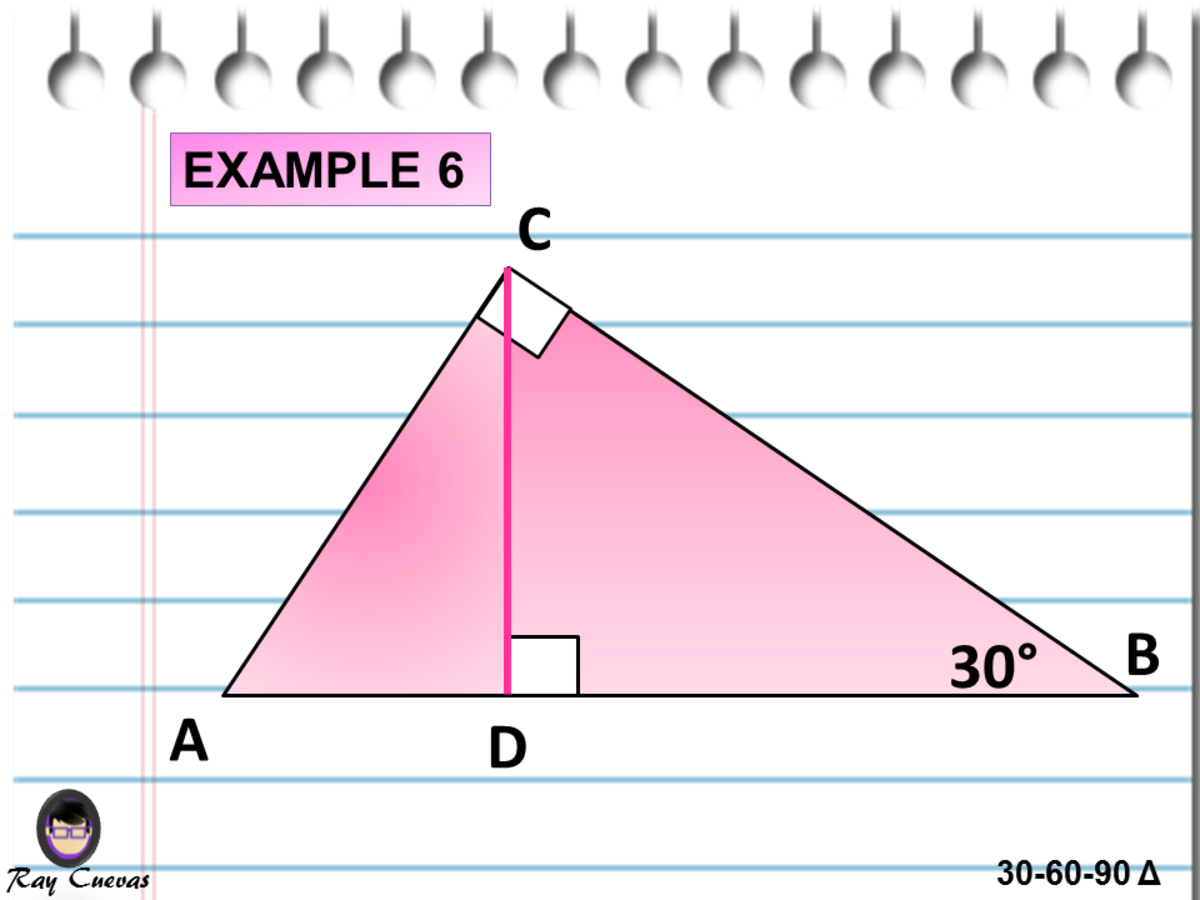



A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation
In any triangle, you see the following The shortest leg is across from the 30degree angle, the length of the hypotenuse is always double the length of the shortest leg, and you can find the length of the long leg by multiplying the short leg by the square root of 3A 30 60 90 triangle completes an arithmetic progression 3030=6030 =90 An arithmetic progression is a sequence of numbers in which the difference of any two successive numbers is a constant For instance, 2,4,6,8 is an arithmetic progression with a constant of 2A triangle is a right triangle with angle measures of 30º, 60º, and 90º (the right angle) Because the angles are always in that ratio, the sides are also always in
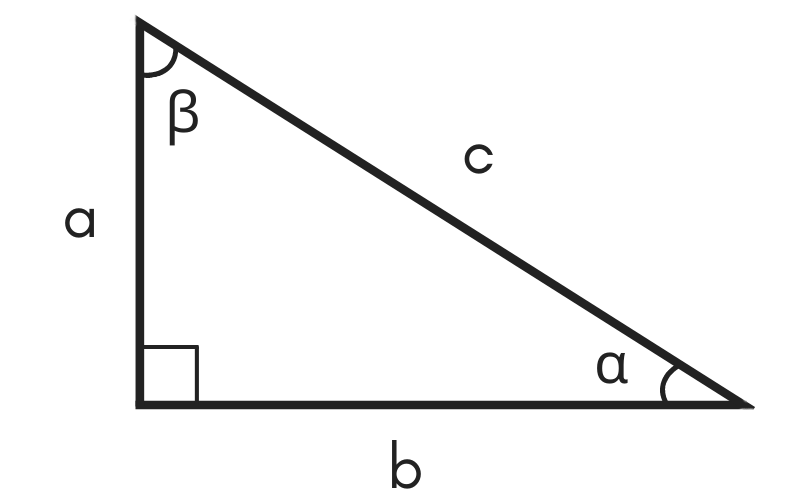



30 60 90 Special Right Triangle Calculator Inch Calculator




30 60 90 Triangle Calculator Formula Rules
Triangle 30 60 90 Calculator This is a special right triangle having 30, 60, and 90 angles from all sides In order to perform specific calculations regarding this type of triangle, you can take the support of different branches of mathematics including trigonometry Triangle 30 60 90 Calculator Formula



1



1




Learn About The 30 60 90 Triangle Caddell Prep Online




Special Right Triangles 30 60 90 And 45 45 90 Triangles Youtube
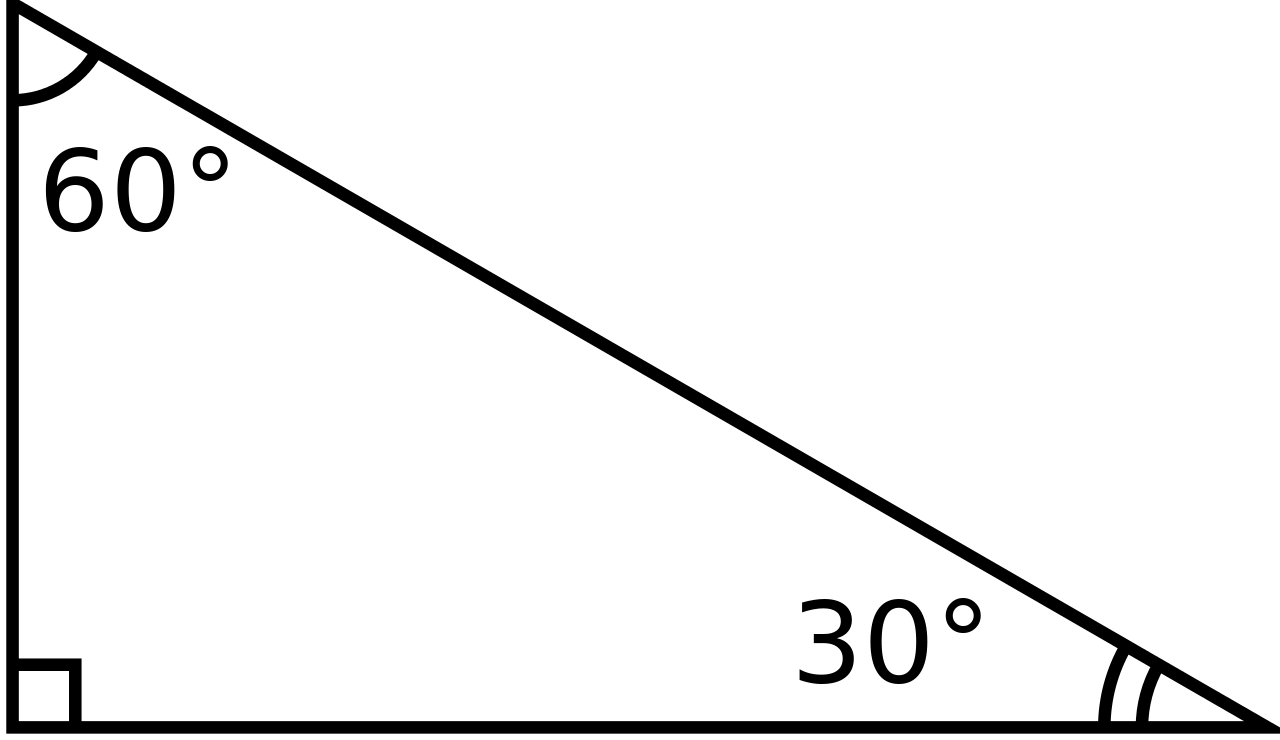



File 30 60 90 Triangle 2 Svg Wikimedia Commons




A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation




How To Work With 30 60 90 Degree Triangles Education Is Around



The Easy Guide To The 30 60 90 Triangle



The Easy Guide To The 30 60 90 Triangle




30 60 90 Right Triangles Solutions Examples Videos




30 60 90 Right Triangles Solutions Examples Videos



The Easy Guide To The 30 60 90 Triangle



30 60 90 Triangle Rules




30 60 90 Triangle Theorem Ratio Formula Video




30 60 90 Triangle Definition Theorem Formula Examples
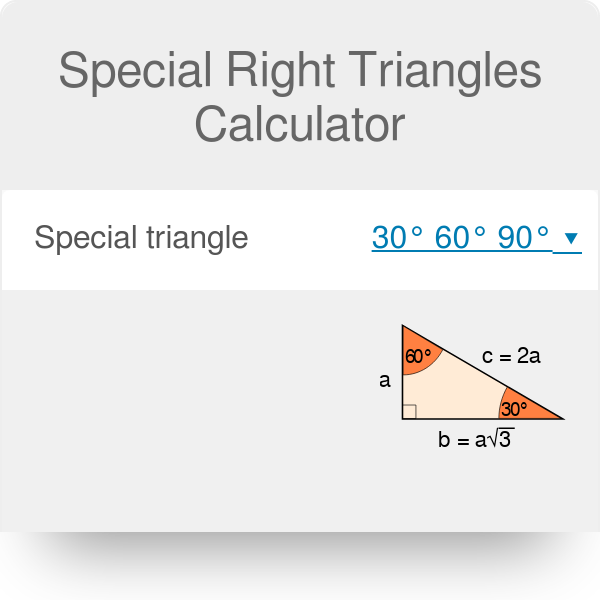



Special Right Triangles Calculator Formula Rules




30 60 90 Special Right Triangle Calculator General Knowledge Book Right Triangle Electrical Engineering Books



1




30 60 90 Triangle Theorem Ratio Formula Video




30 60 90 Triangle Rules Sides Ratio Of A 30 60 90 Triangle Video Lesson Transcript Study Com
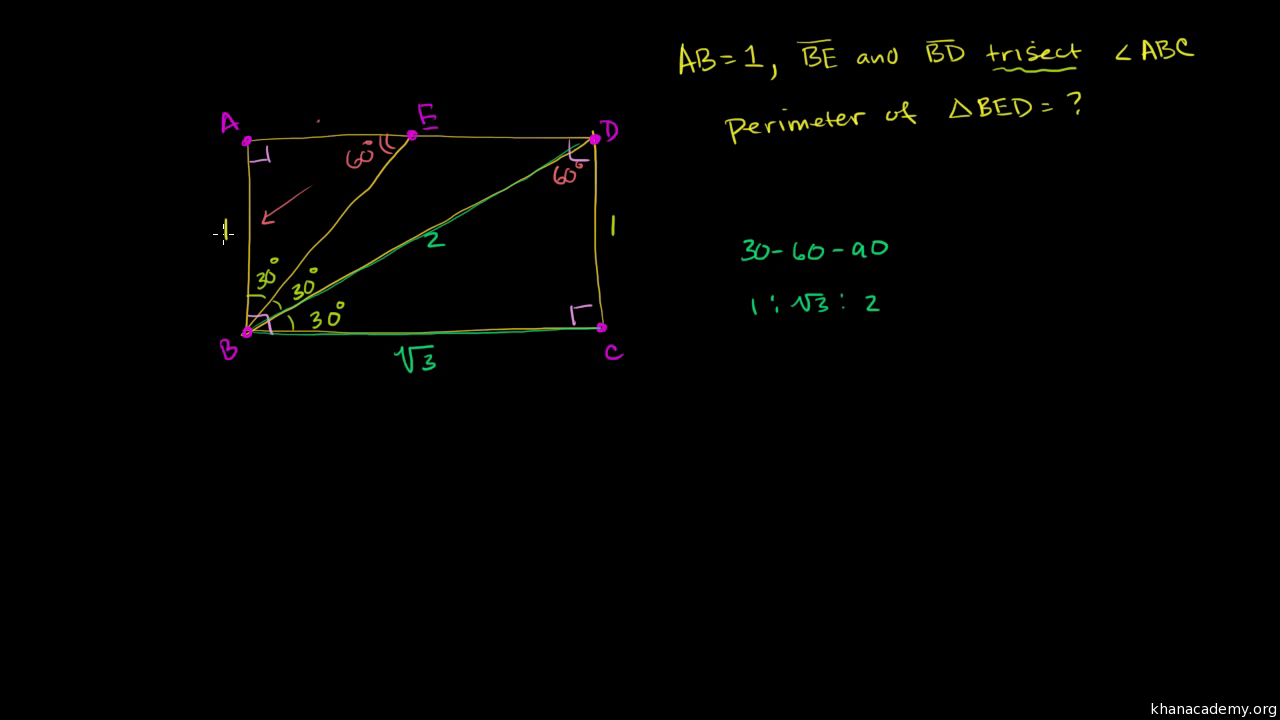



30 60 90 Triangle Example Problem Video Khan Academy



The Easy Guide To The 30 60 90 Triangle



30 60 90 Triangle Definition Theorem Formula Examples



Solve A 30 60 90 Triangle With Gradea
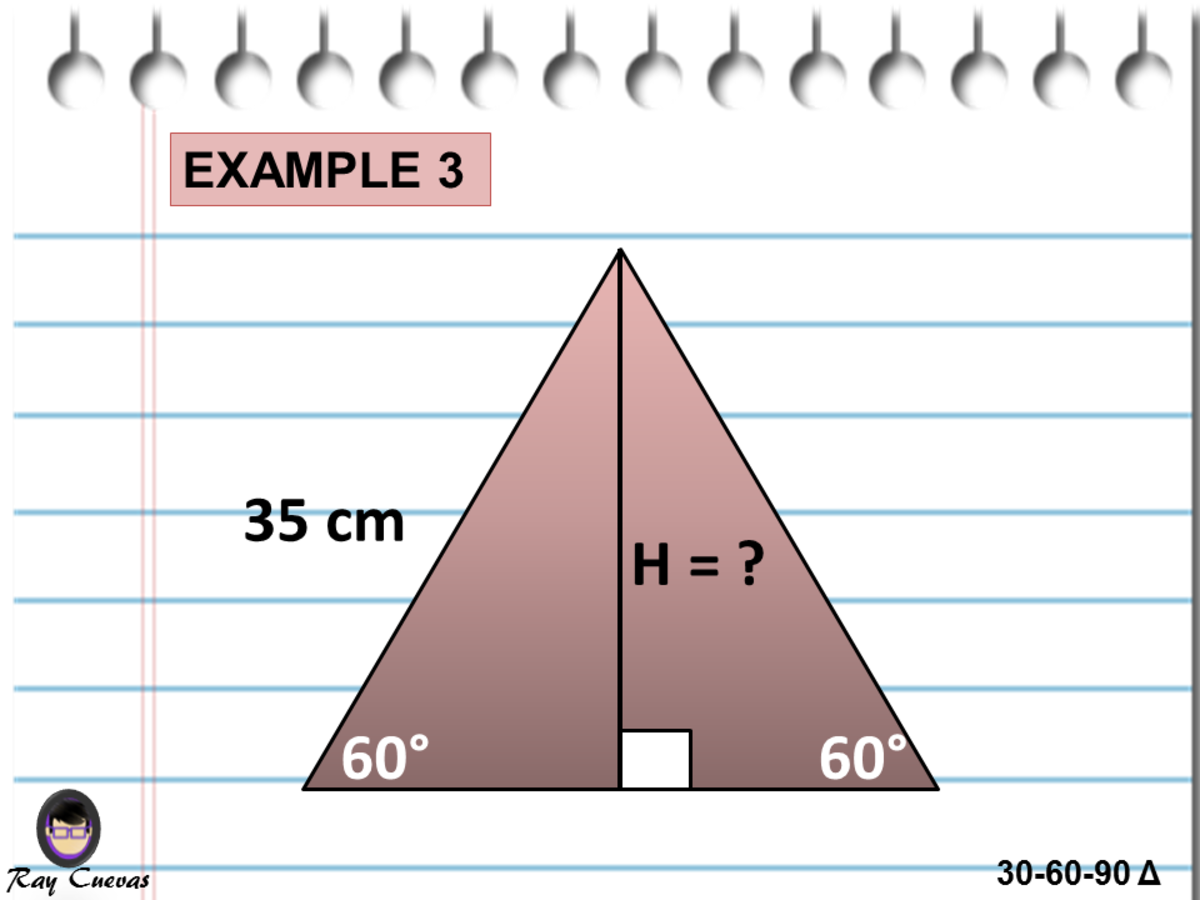



A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation




30 60 90 Triangles




Special Right Triangles Video Lessons Examples And Solutions
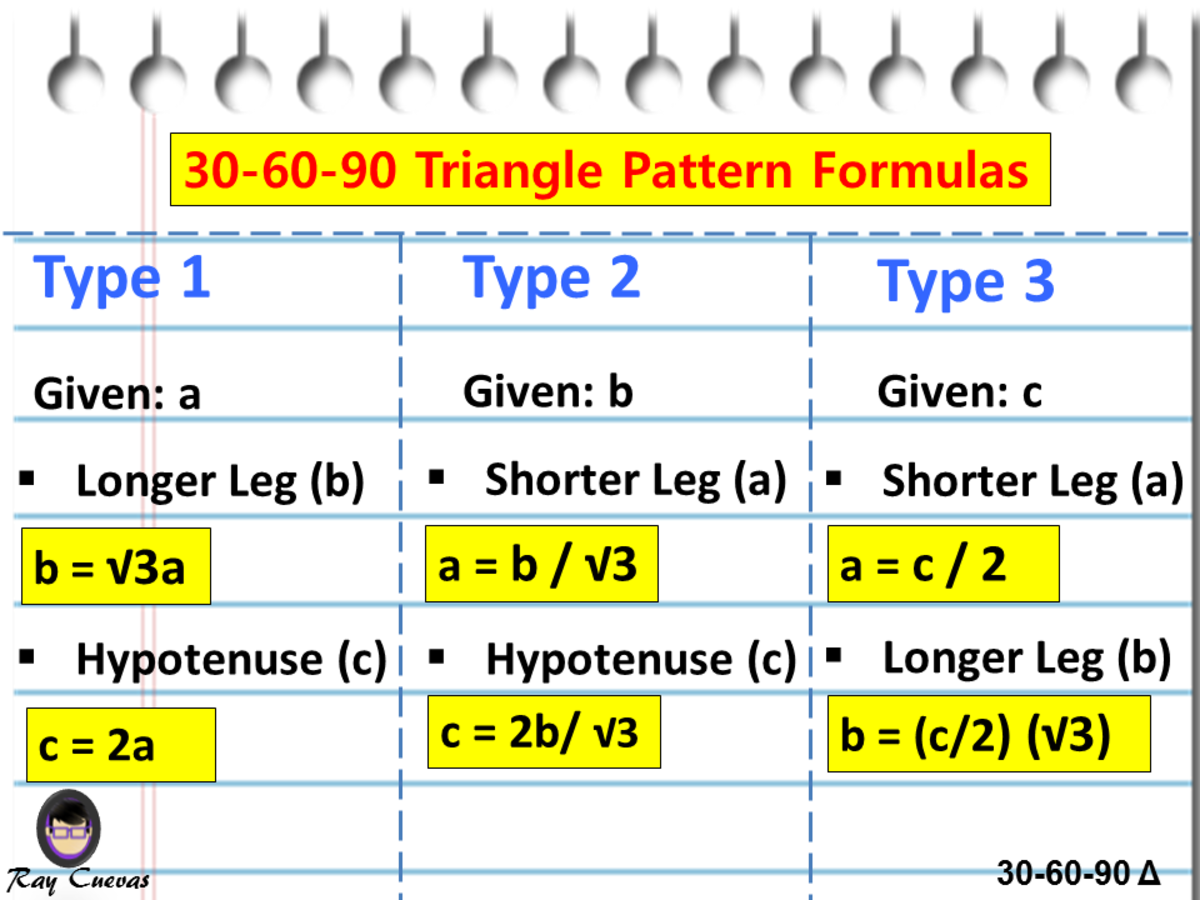



A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation



1




Geometry 8 4 Special Right Triangles This Is
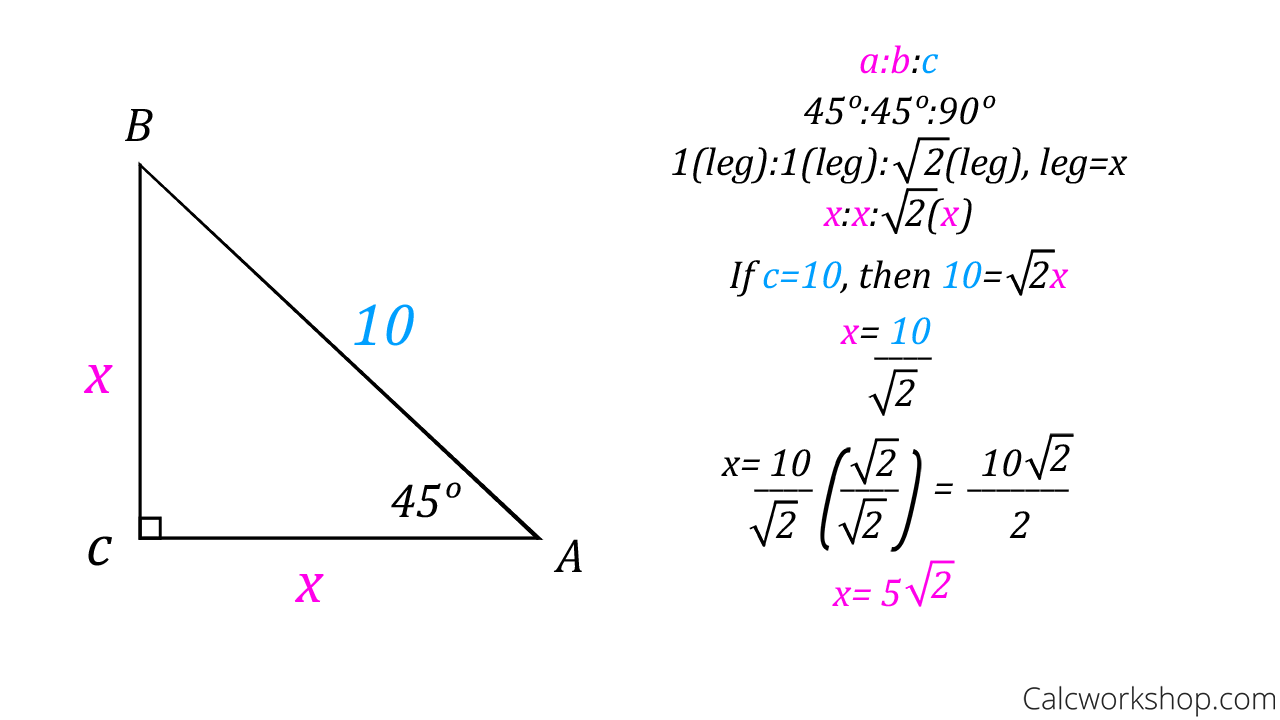



Special Right Triangles Fully Explained W 19 Examples



Special Right Triangles Geometry




30 60 90 Triangle Theorem Properties Formula Video Lesson Transcript Study Com




30 60 90 Triangle Definition Theorem Formula Examples




Special Right Triangles Review Article Khan Academy



45 45 90 And 30 60 90 Triangles Zona Land Education
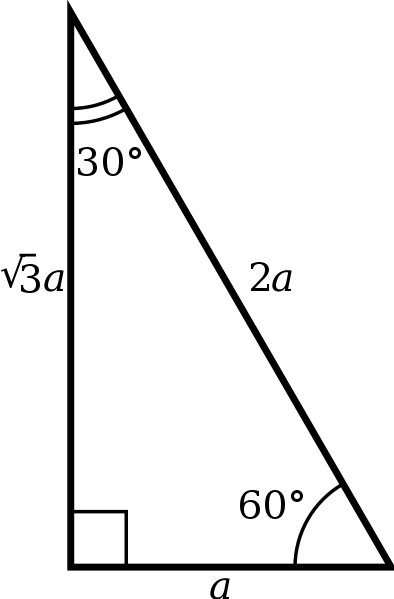



30 60 90 Triangle Formulas Rules And Sides Science Trends
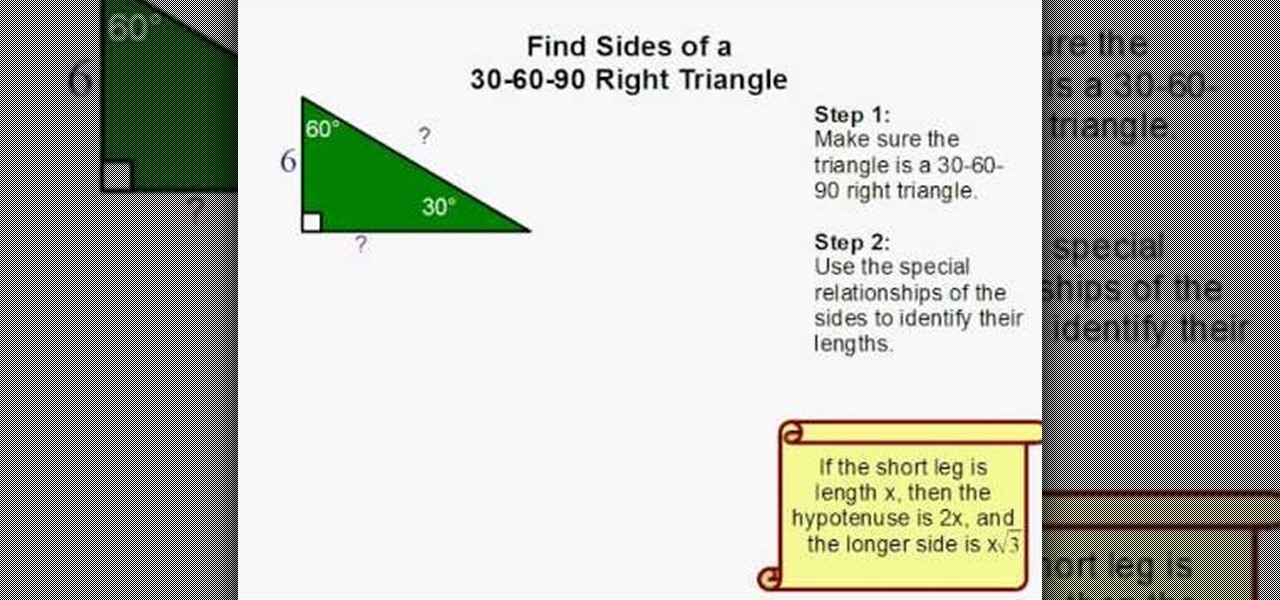



How To Find The Sides Of A 30 60 90 Right Triangle Math Wonderhowto




30 60 90 Triangles Hd Youtube
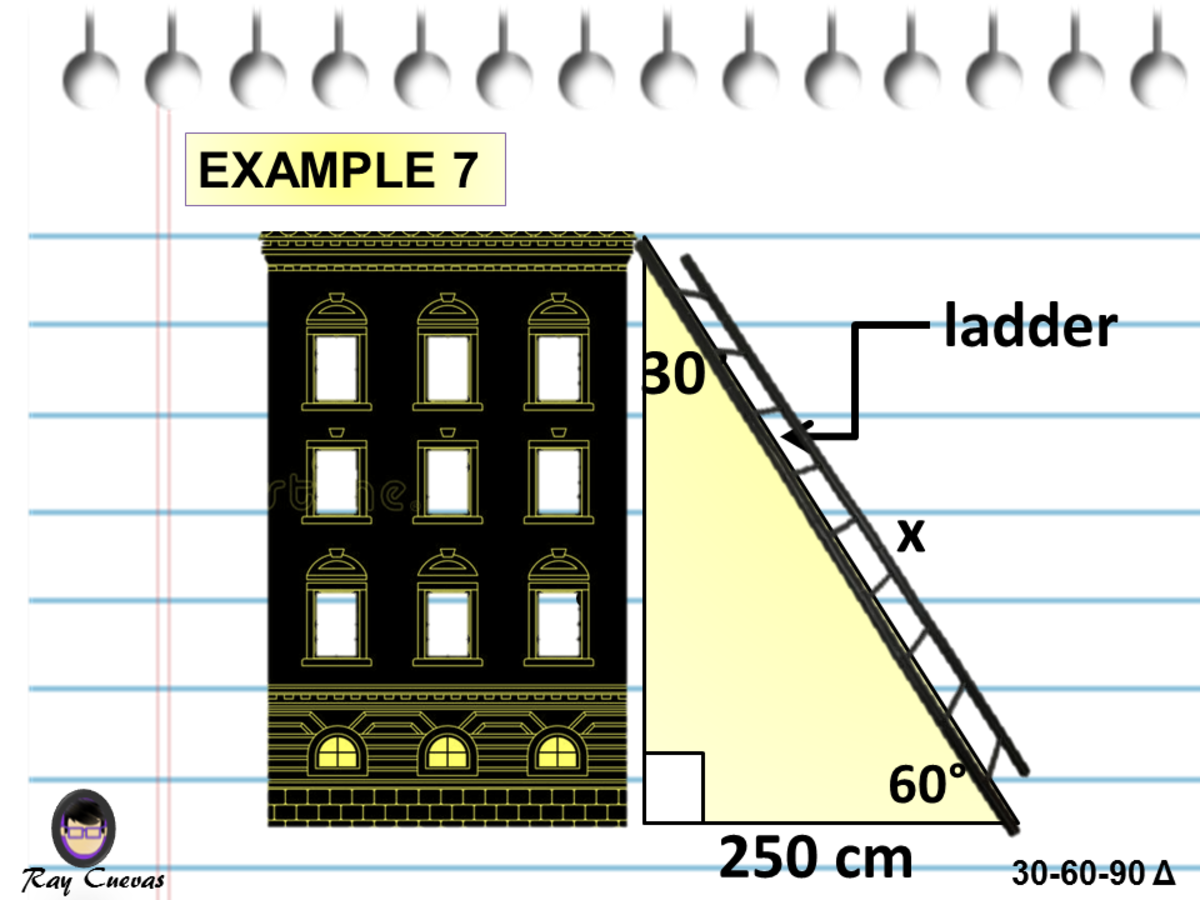



A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation




30 60 90 Triangle Calculator Formula Rules
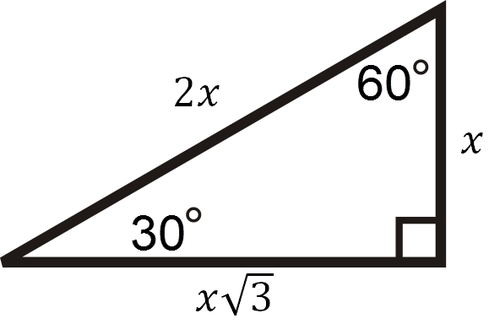



Special Right Triangles Read Geometry Ck 12 Foundation




A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation
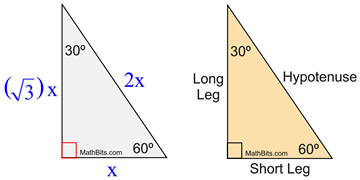



Special Right Triangle 30 60 90 Mathbitsnotebook Geo Ccss Math




30 60 90 Triangle Explanation Examples




30 60 90 Triangle Theorem Proof Don T Memorise Youtube
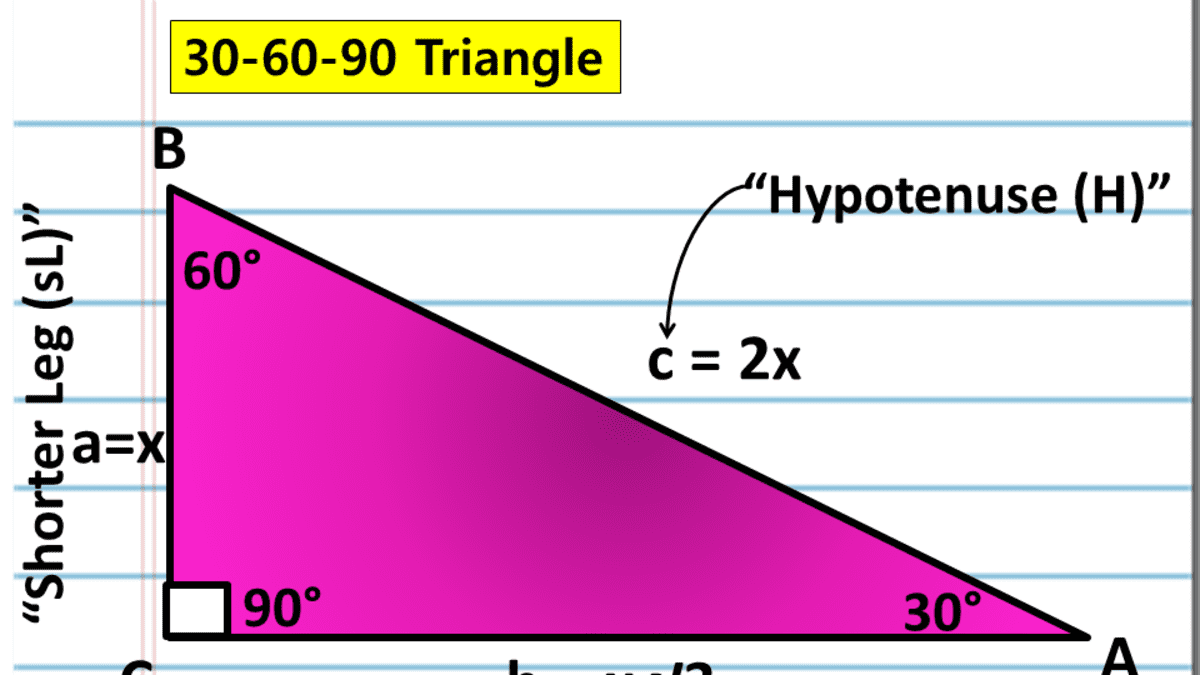



A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation
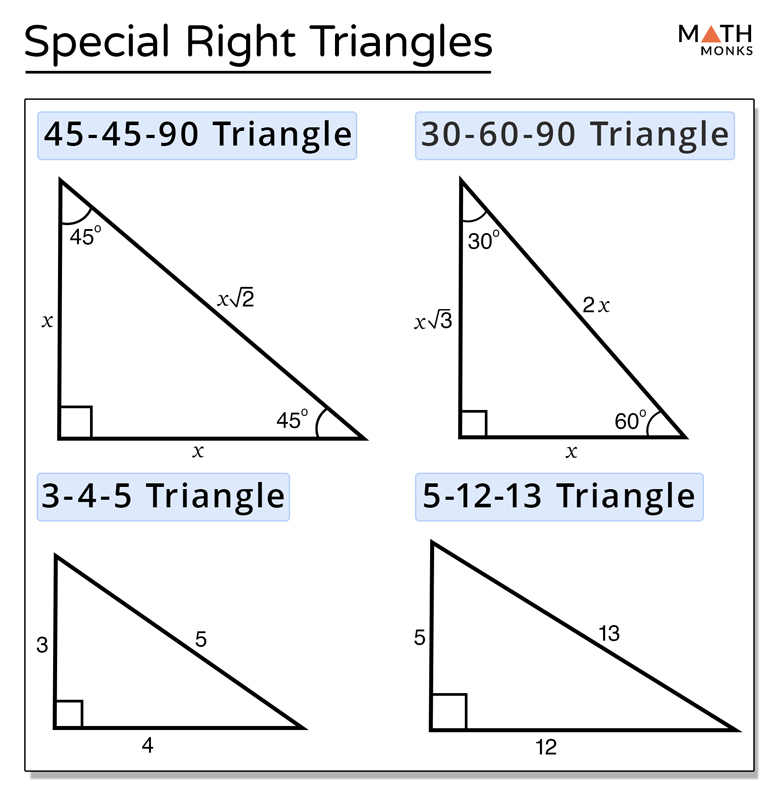



Special Right Triangles Definition Formula Examples




The Converse Of The Pythagorean Theorem And Special Triangles Geometry Right Triangles And Trigonometry Mathplanet



Right Triangle Formulas Xgeometry
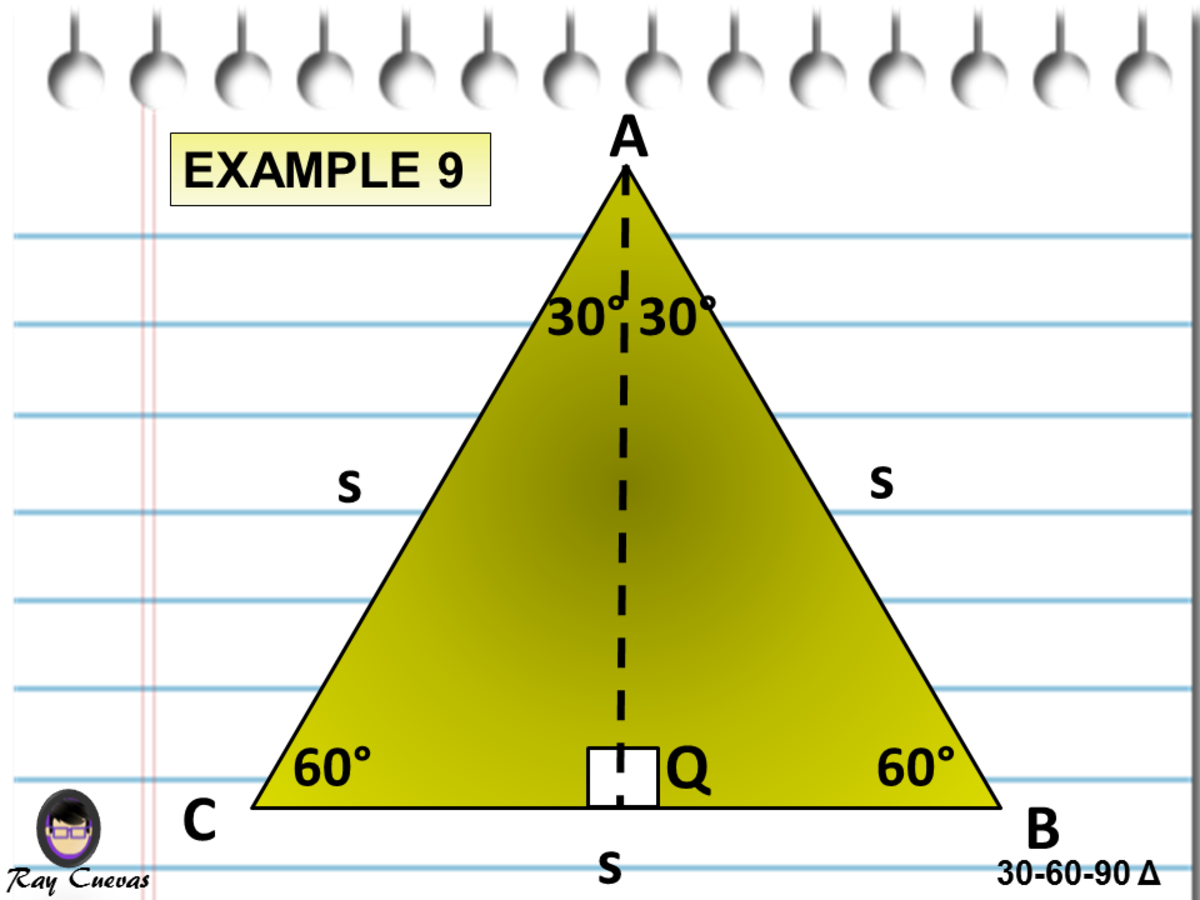



A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation




Right Triangles Interactive Notebook Pages Mrs E Teaches Math




Special Right Triangles Interactive Notebook Page Math Methods Teaching Geometry Teaching Math




Special Right Triangles Fully Explained W 19 Examples




Special Right Triangles Formulas 30 60 90 And 45 45 90 Special Right Triangles Examples Pictures And Inte Learning Mathematics Triangle Formula Math Formulas




30 60 90 Triangle Calculator Formula Rules




30 60 90 Triangle Theorem Properties Formula Video Lesson Transcript Study Com




30 60 90 Triangle Theorem Ratio Formula Video




Special Right Triangles Formulas 30 60 90 And 45 45 90 Special Right Triangles Examples Pictures And Practice Problems




Right Triangles Interactive Notebook Pages Mrs E Teaches Math
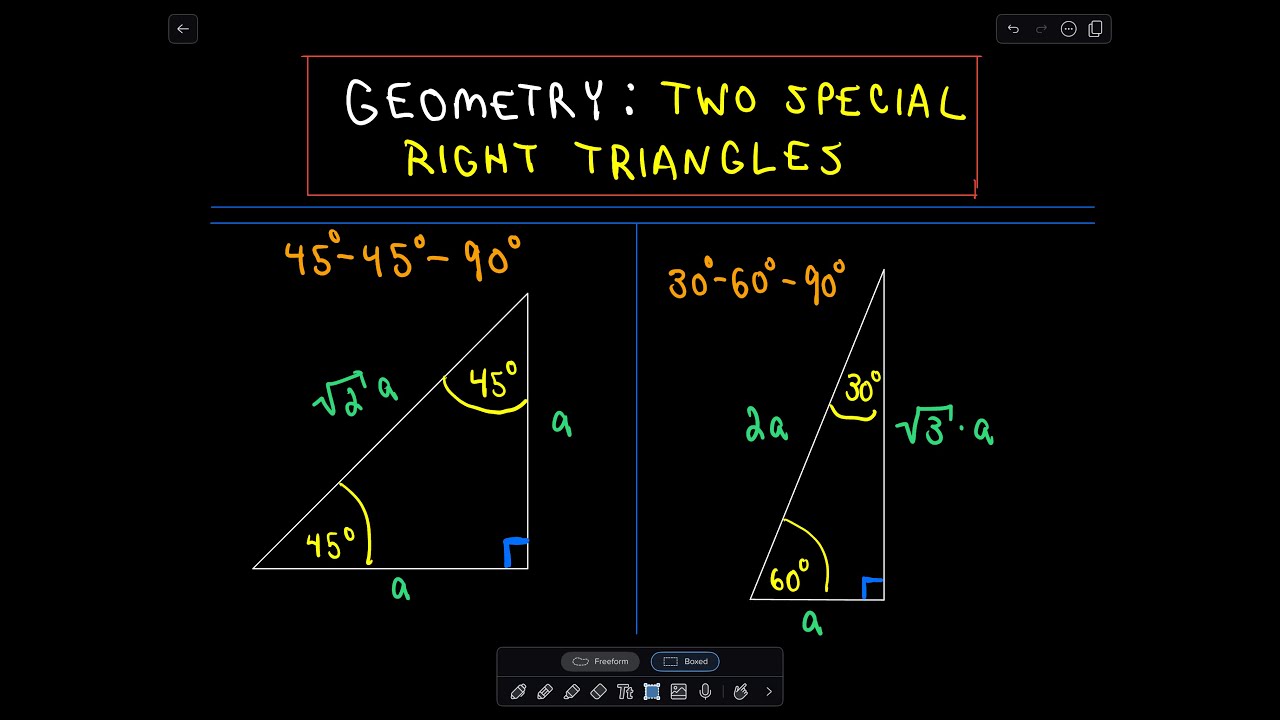



Special Right Triangles In Geometry 45 45 90 And 30 60 90 Youtube




30 60 90 Triangle Theorem Ratio Formula Video




30 60 90 Triangle Theorem Ratio Formula Video




Special Right Triangle Wikipedia




30 60 90 Triangle Theorem Ratio Formula Video




30 60 90 Right Triangles Free Math Help




5 30 60 90 Triangles Geometry15a



The Easy Guide To The 30 60 90 Triangle




The Complete Guide To The 30 60 90 Triangle




A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation




30 60 90 Triangle Theorem Properties Formula Video Lesson Transcript Study Com




The Complete Guide To The 30 60 90 Triangle




30 60 90 Triangle Definition Theorem Formula Examples




Special Right Triangles 45 45 30 60 90 Notes Sheet Graphic Organizers




Special Right Triangles Review Article Khan Academy
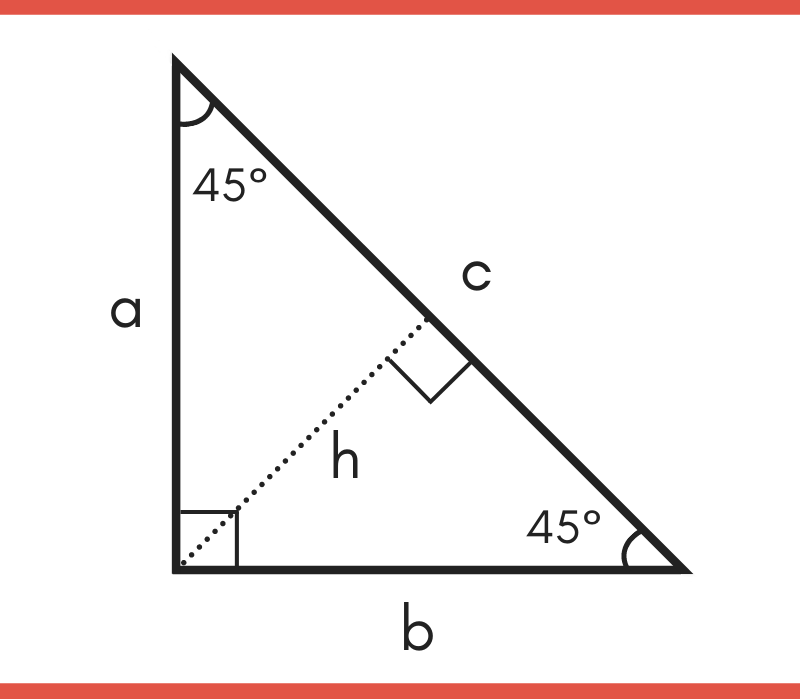



45 45 90 Special Right Triangle Calculator Inch Calculator



My College Options Triangles




A Quick Guide To The 30 60 90 Degree Triangle Dummies




Special Right Triangles Part 1 45 45 90 And 30 60 90 Youtube




30 60 90 Triangle Calculator Formula Rules



0 件のコメント:
コメントを投稿